Folding -- from Wolfram MathWorld
By A Mystery Man Writer
Description
There are many mathematical and recreational problems related to folding. Origami, the Japanese art of paper folding, is one well-known example. It is possible to make a surprising variety of shapes by folding a piece of paper multiple times, making one complete straight cut, then unfolding. For example, a five-pointed star can be produced after four folds (Demaine and Demaine 2004, p. 23), as can a polygonal swan, butterfly, and angelfish (Demaine and Demaine 2004, p. 29). Amazingly, every
graphs and networks - How to use Mathematica to calculate number

Why is pi in the equation for paper folding? - Quora

Wolfram Mathworld in the Notebook Archive

The Magic of Euler's Equation: V-E+F=2. An Eye Opener.
Is Stephen Wolfram's principle of computational equivalence simply

The satisfying math of folding origami - Evan Zodl
Tetrahedron, Ultimate Pop Culture Wiki

code golf - Draw A Reuleaux Triangle! - Code Golf Stack Exchange
National Museum of American History

modular kirigami Flotsam and Origami Jetsam

k-Göbel sequences - by Richard Green
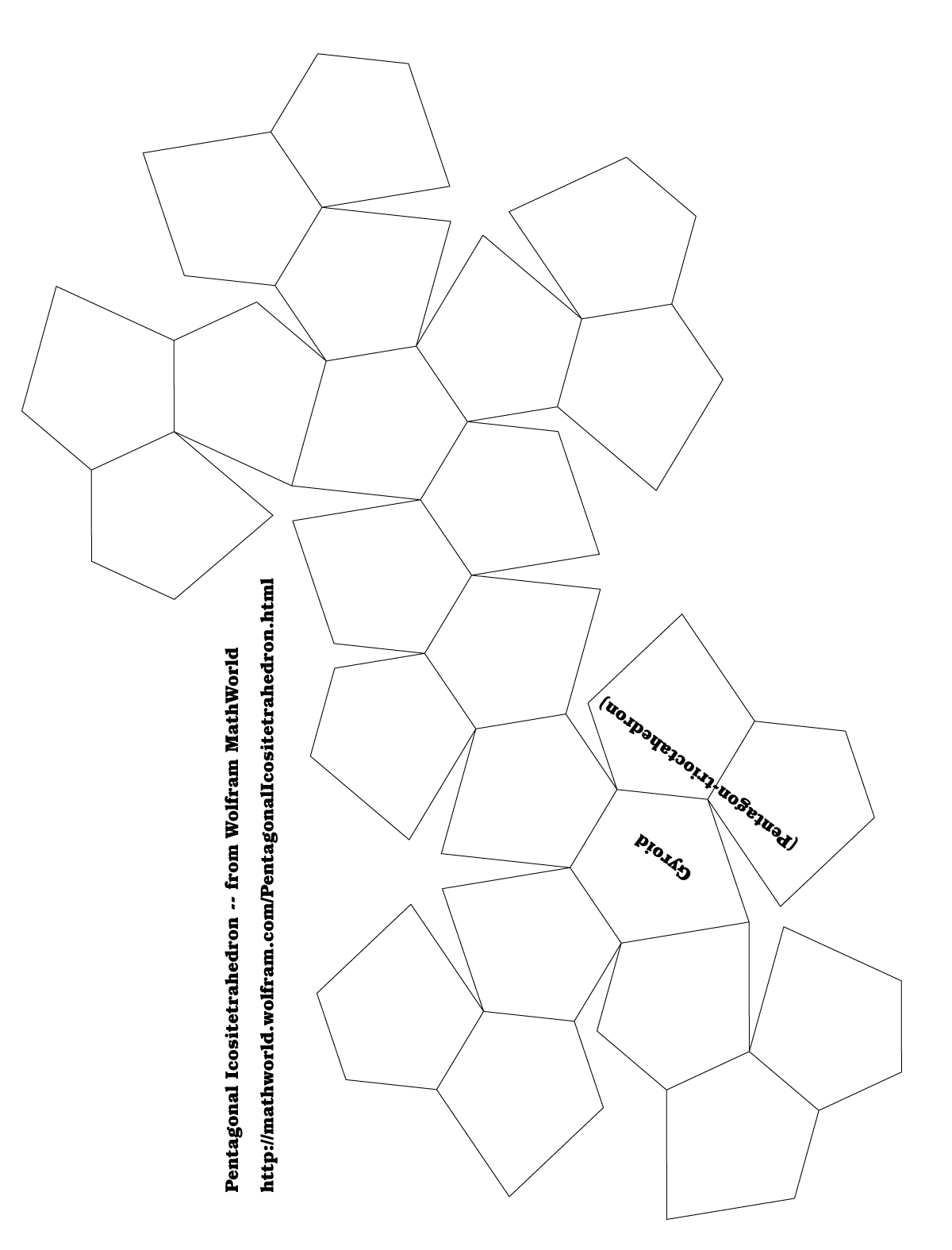
Isometric Class, Crystal Forms, Paper Models
Mathematics, Free Full-Text

Fermat's Library on LinkedIn: The formula for the minimal length

Folding -- from Wolfram MathWorld
from
per adult (price varies by group size)